More trivia:

Green sunshade and shadow

Observation:

There is a bus-stop with a green sunshade on Lancer’s Road that I pass every day. On sunny mornings, I noticed that the shadow under the sunshade was greenish. What was less clear was this: the green hue was most visible when I was some distance away and looking at the bus stop. But the closer I got to the bus stop, the fainter the green became – until it was barely noticeable when I was just under the sunshade. As I walked away from the bus stop, the same sequence occurred, in reverse. When I was again some distance away, the green shadow again became visible.

This puzzling green shadow did not occur on cloudy days, or in the afternoon. So clearly it had something to do with the direct sunshine falling on the sunshade, and not on diffuse scattered sunlight.

The 'sunshade' is standard green fibreglass.

Possible explanation:

a) the fibreglass looks green in reflection because all other colours are absorbed.

b) in transmission, which is what gives the green shadow, the incident, unabsorbed green light is scattered.

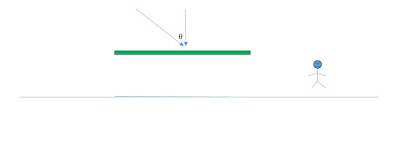
When sunlight is incident vertically on the sunshade, it traverses the minimum thickness t of the sunshade.

When the ray is incident at an angle q to the vertical, it passes through a thickness t /cos (q). This is, as expected, a minimum value t for q = 0, and increases as q increases.

So as the ray becomes more oblique, it passes through a greater thickness of the sunshade and becomes a darker green.

When I observe the ground under the sunshade from a distance, the rays that are visible to the eye are oblique and dark green, and when I am directly under the sunshade, the rays are vertical, and a very pale green.

This assumes that the sunshade is made of a homogenous translucent material and that it is optically isotropic.

According to the link:

http://aces.nmsu.edu/pubs/_circulars/circ556.html

polyethylene and fiberglass tend to scatter light, while acrylic and polycarbonate tend to allow radiation to pass through directly.

The angle of the ray determines the amount of scattering (because of t/cos(q)) and the more intense green occurs at oblique angles of incidence.

The amount of light transmitted through the sunshade is given by:

t = exp(- (α_s+ α_a) l )

where l = t/cos(q) is the path-length of the ray, α_s is the scattering coefficient and α_a is the absorption coefficient. For green, α_a = 0, and α_s ¹0, while for other colours in the visible α_a ¹0.

The scattering through the sunshade is exactly analogous to the enhancement of the redness of sunset rays as the sun dips below the horizon, due to the increased path-length of the oblique sun-rays.

Ok, so 9 months later here are a few corrections, as promised:

Corrections:

(i)                  Including the mass of striker (by just adding it to the mass of the wind sail):

a)      Metal striker: R= 20 mm & t = 8 mm

M_s = r (pr²t) = 8 (3.14)(2²)(0.8) = 80 gms = 0.08 kg

Without including the mass of the striker the min speed is:  2.86 m/s i.e. 10.3 kph

Including the mass of the striker, the min speed is: 3.5 m/s i.e. 12.6 kph

b)      Bamboo striker:

Similarly,

M_s = r (pr²t) = 0.5 (3.14)(2²)(2.2) = 13 gms = 0.013 kg

Without including the mass of the striker the min speed is:  1.21 m/s i.e. 4.34 kph

Including the mass of the striker, the min speed is: 2.38 m/s i.e. 8.56 kph

Note: if the striker mass is included, the effective length L should decrease, because of a shift in the position of the centre of mass – but luckily it does not come into the formulas at all!

(ii)                 Chimes were assumed to be immobile: how good is that approximation, or is it even valid?

Effective area of chime:  A_ch = prL/2 = (3.14)(0.85)(36)/2 = 48.0 cm²

Volume of chime: V_ch = p [(r₁ )²-(r₂)²] L = (3.14)(0.85² – 0.70²) = 26 cc

Mass of chime m_ch = r V_ch = (8)(26) =210 gms = 0.21 kg

Force of gravity on chime: F = mg = (9.8)(0.21) = 2.06  Nt

Force due to wind at 10 kph (2.78 m/s):  F =  A_ch ( r_air v²)/2 = (0.0048)(1.2)(2.78)²/2  =  0.022   Nt

F/mg = 0.022/2.06 = 0.0108

mg/F = 92.6

h = 2L/(1 + 92.6²) = 2(0.75)/8573 = 1.75x10^-4 m = 0.175 mm.

Tan(q/2) = F/mg = 0.0108 q = 1.24°.

For a chime, the centre of mass is at L/2, so this height and angle should be half (0.088 mm and 0.62°).

(iii)               Angular issues:

Another issue which was not mentioned earlier is the angular factor, taking into account the number of chimes. In the metal chimes that I have, there are 5 chimes, so that a top view  would show a 72° angular separation between adjacent chimes when they are at rest. The bamboo chimes have 6 chimes, so the angular separation between adjacent chimes is 60° (as shown in the above figure). In the preceding derivation, the striker is assumed to move away from the centre along a radius, and it is also assumed that the chime is also located on the same radius – a case of motion along a line. However, the striker may also move in a direction that takes it along a radius that is midway between two adjacent chimes – or, indeed, at an arbitrary angle. The displacement x_m was earlier calculated using the linear case. The most general case, if the striker moves at an arbitrary angle, is more difficult – but the case in which it moves midway between two adjacent chimes is not so tough. In the above figure, the striker (of radius s) moves a distance d, till it hits both chimes (of radius c) simultaneously. In the figure above, there are 6 chimes, so the positions of the chimes are separated by 60°.

In the case of linear motion (discussed previously), the condition for the striker to touch the chime is:

d₁ + s + c = r

where r is the radius of the circle on which the centres of the 6 chimes are located.

Now consider the case in which the striker moves midway between adjacent chimes in the figure above. Using the cosine law, the condition for the striker to touch both chimes at once is:

(s+c)² = (d₂)² + r² – 2d₂r  cos(q)

where 2q = 60°.

One can plug in the numbers for s, c and r and solve the quadratic to obtain the displacement d. This can displacement then be put into the previously calculated x_m and find the wind-speed that will cause contact between the striker and the chime.

Solving the quadratic:

d₂ = - rcos(q) + ((rcos(q))² + (s+c)²)^1/2

Is d₁ or d₂ greater? That depends on the specific values of r,s,c and q - it could go either way.

If the displacement required is greater in the midway case (d₂) than it is in the linear case (d₁), then the wind-speed is also higher in the midway case (and vice versa). For the case of 6 chimes, the plot of v(q) should exhibit six-fold symmetry; and for 5 chimes, it will exhibit five-fold symmetry.

(iv)              Miscellaneous:

Here it is assumed that the material of the chimes, the striker, and the wind sail (bob) are all the same. To alleviate this problem, the density of the bob & striker should be lower than that of the chimes. Apparently, the material of the striker is different, but the chimes and the bob seem to be of the same material in the metal chimes.

The Bali bamboo chimes have another odd problem: the chimes are not kept hanging vertically down: they are at about 10-15° away from the vertical, pointing radially outward from the bob/striker at the centre.